Merge Sort in C++ | Explanation with Example

Introduction

Merge Sort is a classic sorting algorithm that employs the "divide and conquer" paradigm. It is an efficient, stable, and comparison-based algorithm that breaks down a list into smaller sub-lists, sorts those sub-lists, and then merges them back together. Here’s a comprehensive explanation of how Merge Sort works in C++, along with an illustrative example.

How Merge Sort Works

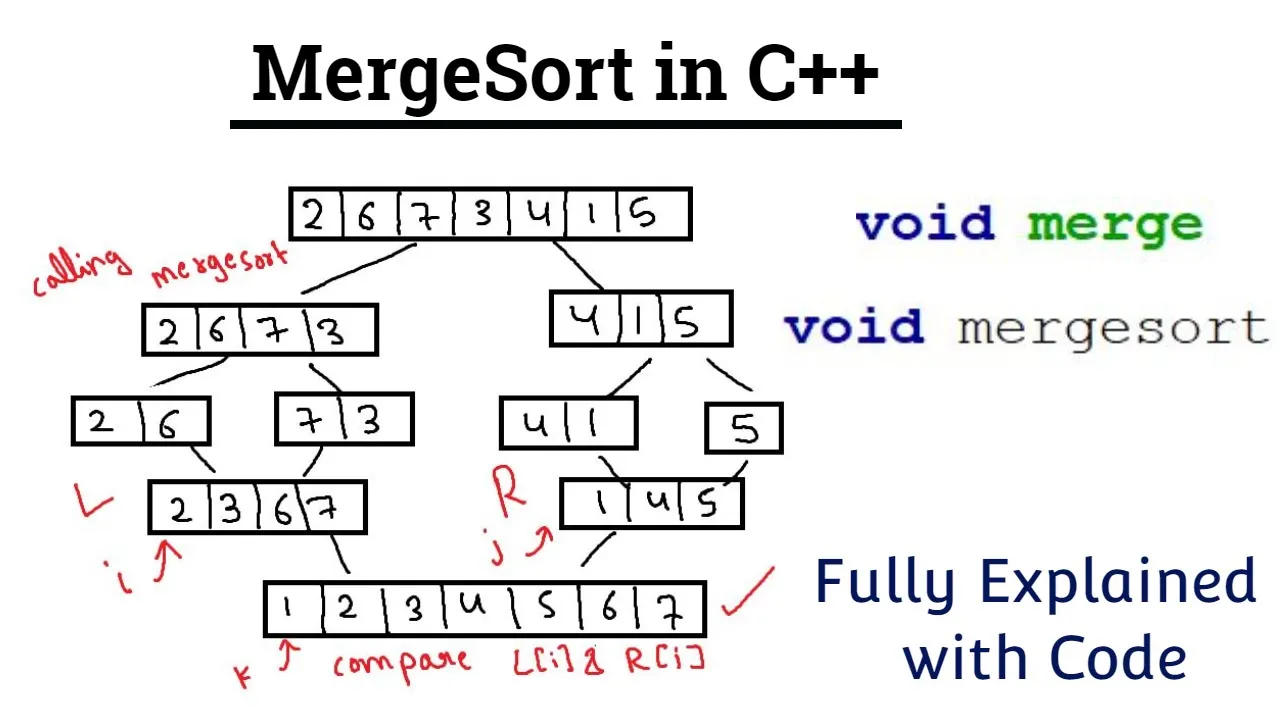
Step 1: Divide

The first step involves dividing the unsorted list into n sub-lists, each containing one element. Since a list with one element is considered sorted, we start by dividing the main list progressively until we reach single-element sub-lists.

Step 2: Conquer

Once the list is divided, the merging process begins. The algorithm recursively sorts each half of the list. This involves comparing the elements of each sub-list and arranging them in the correct order.

Step 3: Merge

After the sorting is complete, the process combines the sorted sub-lists back into one complete sorted list. The merging phase continues until all the sub-lists are merged back into a single sorted list.

C++ Implementation

Below is an example implementation of Merge Sort in C++:

#include <iostream>
#include <vector>

// Function to merge two halves of a vector
void merge(std::vector<int>& arr, int left, int mid, int right) (
    int n1 = mid - left + 1;
    int n2 = right - mid;
    
    std::vector<int> L(n1);
    std::vector<int> R(n2);
    
    for (int i = 0; i < n1; i++)
        L[i] = arr[left + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[mid + 1 + j];
    
    int i = 0;
    int j = 0;
    int k = left;
    
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        ) else (
            arr[k] = R[j];
            j++;
        )
        k++;
    }
    
    while (i < n1) (
        arr[k] = L[i];
        i++;
        k++;
    )
    
    while (j < n2) (
        arr[k] = R[j];
        j++;
        k++;
    )
}

// Function to implement merge sort
void mergeSort(std::vector<int>& arr, int left, int right) (
    if (left < right) {
        int mid = left + (right - left) / 2;

        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    )
}

// Main function to demonstrate merge sort
int main() (
    std::vector<int> arr = {38, 27, 43, 3, 9, 82, 10);
    int arr_size = arr.size();

    std::cout << "Given array: ";
    for (int i = 0; i < arr_size; i++)
        std::cout << arr[i] << " ";
    std::cout << std::endl;

    mergeSort(arr, 0, arr_size - 1);

    std::cout << "Sorted array: ";
    for (int i = 0; i < arr_size; i++)
        std::cout << arr[i] << " ";
    std::cout << std::endl;

    return 0;
}

In this code, we implement the merge() function to combine two sorted sub-arrays into a single sorted array and the mergeSort() function to sort the entire array recursively.

Keyword

• Merge Sort
• C++
• Sorting Algorithm
• Divide and Conquer
• Recursion
• Merging
• Arrays
• Implementation
• Code Example

FAQ

Q1: What is Merge Sort?
A1: Merge Sort is a sorting algorithm that follows the divide and conquer approach to sort elements by dividing the array into smaller sub-arrays, sorting them, and then merging them back together.

Q2: Is Merge Sort efficient?
A2: Yes, Merge Sort has a time complexity of O(n log n), making it efficient for larger datasets compared to simpler algorithms like Bubble Sort.

Q3: What are the advantages of Merge Sort?
A3: Merge Sort is stable, meaning it maintains the relative order of equal elements. It is also suitable for larger datasets and is preferred for sorting linked lists.

Q4: How does Merge Sort differ from Quick Sort?
A4: While both algorithms utilize divide and conquer, Merge Sort consistently divides the array into two halves and is stable, whereas Quick Sort selects a pivot element and sorts elements around it, which may lead to unstable sorting.

Q5: Can Merge Sort be used for linked lists?
A5: Yes, Merge Sort is often used for linked lists as it does not require random access and can run efficiently with linked data structures.